標題:減少卷積神經網路的層數,參數量就一定會減少嗎?答案可能相反!
前言:
在建置影像的卷積神經網路模型時,過度配適(過擬合,overfitting)的現象常常在樣本數不足的情況出現,除了想辦法透過資料擴增或遷移學習的方法解決這個問題外,神經網路的模型參數量過大往往是更容易造成此問題的重要因素。
但是,不少初學者透過減少"卷積層及池化層"的方式減少模型的大小,但是這個動作在"某些情況"反而造成模型的參數量更大。
本文透過實際計算參數量的方式,講述"減少卷積層及池化層"時"參數量反而越來越大"的情況。
-----------分隔線-----------
卷積運算的介紹:
卷積運算相當於濾鏡運算,簡單來說,我們用下圖的例子作為範例。
這是常見的卷積運算,但如果是有3個色板的RGB影像,該如何計算呢,請見下圖。三個色板,進行了三種不同的卷積核(kernel)的運算後,加在一起,這時,神經網路需要更新的參數量為27(3個色板乘上3×3的kernel)個,也就是說,無論影像多大,卷積層的參數量都不變。
如果第一層卷積層的輸出為32個色板,那麼,上面這張圖的運算就會有32次,再將這32個輸出合併為同一個張量的32個色板,不過這32次卷積運算中,參數的數值會不同。
在這裡,參數量為3×(3×3)×32=864(與圖片大小無關)
如果第二層卷積層的輸出為64個色板,那麼,就可以想像成,上面那張圖的左邊有32個4×4大小的圖片,再乘上3×3大小的核(kernel),由於這個動作只會輸出一個色板,所以類似此運算會做64次。
在這裡,參數量為32×(3×3)×64=18,432(與圖片大小無關)
看到這裡,可能會覺得,卷積神經網路其實是在進行3D的卷積運算(像下圖這樣),其實在實作時通常還是2D的運算。(見更下一張圖)
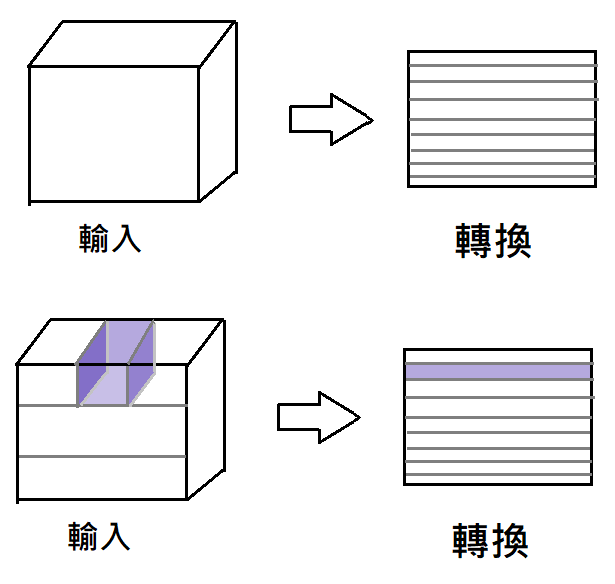
程式庫在進行運算時,通常會將3D的輸入轉換成2D的輸入(如下圖),這樣做的好處,就是能利用線性代數的程式庫讓陣列的計算最佳化。像下圖這樣,將3D的輸入和核都轉成二維矩陣時,就可以透過2維的乘法運算,快速完成3D的卷積運算,算完後再轉換回3D的大小。
然而,為什麼減少神經網路的層數時在部分情況反而會造成模型的參數量更大呢,原因就出在平坦層後方的全連結層。
-----------分隔線-----------
全連結層的矩陣乘積運算:
先看下圖,你可以看到,全連結層的運算模擬圖(輸入的大小為2、隱藏層的神經元大小為3)。
在這裡,看起來,隱藏層的參數量就是6個(不考慮偏權值)。
所以很容易就能看出來,W的數量並不是神經元數量,而是線的數量。
那麼,如果平坦化後的結果是32,768個數字,在下一層的全連結層的輸出有128個神經元時,就會有32,768×128= 4,194,304個參數。
這一層的參數量遠遠比前面所有的卷積運算的參數量加起來都還大。
而這一層的參數量,跟圖片的大小有間接關係。
-----------分隔線-----------
現在來以例子來計算吧。
圖片的輸入為224*224的大小,有RGB三個色板。
模型為:
input→32個filter的3×3濾鏡→2×2池化層→64個filter的3×3濾鏡→2×2池化層→128個filter的3×3濾鏡→2×2池化層→256個filter的3×3濾鏡→2×2池化層→平坦層→128個神經元的全連結層→2個神經元的輸出層。
然後,為了縮減模型的大小,弄巧成拙的減少了一層卷積層和池化層:
input→32個filter的3×3濾鏡→2×2池化層→64個filter的3×3濾鏡→2×2池化層→128個filter的3×3濾鏡→2×2池化層→平坦層→128個神經元的全連結層→2個神經元的輸出層。
兩者的差異如下(不考慮偏權值):
第一個模型的參數量(六百萬個參數):
3×(3×3)×32→0→32×(3×3)×64→0→64×(3×3)×128→0→128×(3×3)×256→0→0→[14×14×256]×128→128×2=864+18,432+73,728+294,912+[6,422,528]+256=6,810,720。
第二個弄巧成拙的模型參數量(一千兩百萬個參數):
3×(3×3)×32→0→32×(3×3)×64→0→64×(3×3)×128→0→0→[28×28×128]×128→128×2=864+18,432+73,728+[12,845,056]+256=12,938,336。
由上述計算可算出,減少了一層卷積層和池化層後,由於能縮減四分之三參數的池化層減少了,少了池化層後,圖片的大小從14×14變成28×28,接上全連結層後,參數量反而增加了。
所以,如果要減少模型的大小,不妨先注意平坦層後方的全連結層。
另外,使用全域平均池化,可以將所有色板直接取平均值,只留下一個數值,這樣的話是能顯著減少那一層的參數量的,這是一個好方法。
真棒,今天又學到了很多東西呢!






沒有留言:
張貼留言
有興趣或有疑問的歡迎提問與交流喔!!!